SEMANA 1
Sucesion
Una sucesi on, representada matem aticamente como fzng, es una funci on cuyo dominio son los enteros positivos (1; 2; 3; 4; : : :); en otras palabras, a cada entero n = 1; 2; 3 : : : se le asigna un n umero complejo zn. Por ejemplo, la sucesi on f1 + ing representar a la funcion.
L imite de una Sucesi on
Se dice que una sucesi on fzng converge al valor L si paracualquier medida de cercan a > 0 existe una posici on no a partir de la cual todos los terminos siguientes de la sucesi on aproximan a L con un error menor que ; es decir, distan de L en menos que E :
SERIES
En matemáticas, una serie es la generalización de la noción de suma a los términos de una sucesión infinita. Informalmente, es el resultado de sumar los términos:  lo cual suele escribirse en forma más compacta con el símbolo de sumatorio:
lo cual suele escribirse en forma más compacta con el símbolo de sumatorio:  .
.
 lo cual suele escribirse en forma más compacta con el símbolo de sumatorio:
lo cual suele escribirse en forma más compacta con el símbolo de sumatorio:  .
.
El estudio de las series consiste en la evaluación de la suma de un número finito n de términos sucesivos, y mediante un pasaje al límite identificar el comportamiento de la serie a medida que n crece indefinidamente.
Una secuencia o cadena «finita», tiene un primer y último término bien definidos; en cambio en una serie infinita, cada uno de los términos suele obtenerse a partir de una determinada regla o fórmula, o por algún algoritmo. Al tener infinitos términos, esta noción suele expresarse como serie infinita, pero a diferencia de las sumas finitas, las series infinitas requieren de herramientas del análisis matemático para ser debidamente comprendidas y manipuladas. Existe una gran cantidad de métodos para determinar la naturaleza de convergencia o no-convergencia de las series matemáticas, sin realizar explícitamente los cálculos.
Series Especiales
Criterios de Convergencia
Criterio de la Razon
Criterio de la Raiz
Radio de Convergencia
Criterio de Comparación
SEMANA 2
Serie de Taylor
En matemáticas, una serie de Taylor es una aproximación de funciones mediante una serie de potencias o suma de potencias enteras de polinomios como  llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto
llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto  suficientemente derivable sobre la función y un entorno sobre el cual converja la serie. Si esta serie está centrada sobre el punto cero,
suficientemente derivable sobre la función y un entorno sobre el cual converja la serie. Si esta serie está centrada sobre el punto cero, 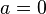 , se le denomina serie de McLaurin.
, se le denomina serie de McLaurin.
 llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto
llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto  suficientemente derivable sobre la función y un entorno sobre el cual converja la serie. Si esta serie está centrada sobre el punto cero,
suficientemente derivable sobre la función y un entorno sobre el cual converja la serie. Si esta serie está centrada sobre el punto cero, 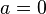 , se le denomina serie de McLaurin.
, se le denomina serie de McLaurin.
Esta aproximación tiene tres ventajas importantes:
- la derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales;
- se puede utilizar para calcular valores aproximados de funciones;
- es posible calcular la optimidad de la aproximación.
Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x (véase Serie de Laurent). Por ejemplo f(x) = exp(−1/x²) se puede desarrollar como serie de Laurent.
Desarrollo de Serie de Taylor
Ya que no hay funciones elementales para calcular la integral anterior, por lo tanto no se podría escribir la solución en forma cerrada y por consiguiente tendríamos que conformarnos con alguna aproximación numérica.
Apliquemos inicialmente el método de Taylor.
SEMANA 3
Serie de Maclaurin
Dada una serie entera o de potencias, ya nos hemos ocupado del problema de hallar su suma. Ahora, partimos de una función f definida en un intervalo I centrado en el origen y nos planteamos:
¿Existe una serie entera cuya suma sea igual a f en I ?
En caso afirmativo, ¿es única tal serie?
En caso afirmativo, ¿es única tal serie?
Problema de unicidad. Se resuelve afirmativamente con el siguiente teorema:
TEOREMA. Sea I un intervalo abierto centrado en 0 y f una función definida en I. Si f es igual en I a la suma de una serie entera, esta serie es necesariamente
TEOREMA DEL RESIDUO
El teorema de los residuos es consecuencia directa del teorema integral de Cauchy y forma parte fundamental de la teoría matemática de análisis complejo.
Enunciado
Sea  una función analítica en un dominio simplemente conexo
una función analítica en un dominio simplemente conexo  , excepto en un número finito de puntos
, excepto en un número finito de puntos 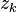 que constituyen singularidades aisladas de
que constituyen singularidades aisladas de  . Sea
. Sea  una curva en
una curva en  , simple, cerrada, regular a trozos, con orientación positiva y tal que el dominio que esta define contiene las singularidades de
, simple, cerrada, regular a trozos, con orientación positiva y tal que el dominio que esta define contiene las singularidades de  . Entonces se tiene:
. Entonces se tiene:
 una función analítica en un dominio simplemente conexo
una función analítica en un dominio simplemente conexo  , excepto en un número finito de puntos
, excepto en un número finito de puntos 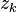 que constituyen singularidades aisladas de
que constituyen singularidades aisladas de  . Sea
. Sea  una curva en
una curva en  , simple, cerrada, regular a trozos, con orientación positiva y tal que el dominio que esta define contiene las singularidades de
, simple, cerrada, regular a trozos, con orientación positiva y tal que el dominio que esta define contiene las singularidades de  . Entonces se tiene:
. Entonces se tiene:
donde  es el Residuo de la función
es el Residuo de la función  en el punto singular
en el punto singular 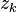 .
.
 es el Residuo de la función
es el Residuo de la función  en el punto singular
en el punto singular 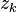 .
.- Enlaces Relacionados:
- http://fernandorevilla.es/serie-de-maclaurin/
- http://es.slideshare.net/FaveeLaNatsuko/serie-detaylorymcl
- Variable Compleja (Murray Spiegel) - Serie Schaum (Imagenes Tomadas).
SEMANA 4
EXPOSICIONES ENLACES:
Grupo 2: Series de Fourier 2015/06/25-2015/06/29
Grupo 3: Series de Fourier de funciones Pares e Impares 2015/06/29-2015/07/02

























No hay comentarios:
Publicar un comentario
abril